Numpy基础¶
概要¶
本文讲解了numpy的一些基础操作. 同时还会介绍numpy中两个重要的概念全局函数与广播. 最后还介绍了numpy下面的两个包, linalg线形代数计算包与random随机生成包.
keywords numpy 初始化 索引 random 随机 线性代数
何为Numpy?¶

NumPy 是一个运行速度非常快的数学库,主要用于矩阵运算。
为什么我们不用python原生的list呢?¶
矩阵运算功能
它可以让你在 Python 中使用向量和数学矩阵,以及封装了很多矩阵运算等操作, 这些都是list所不具备的.
numpy更省空间
NumPy中的数组的存储效率和输入输出性能均远远优于Python中等价的基本数据结构,且其能够提升的性能是与数组中的元素成比例的.
处理速度更快
NumPy的大部分代码都是用C语言写的,其底层算法在设计时就有着优异的性能,这使得NumPy比纯Python代码高效得多.
关于这方面的讨论细节, 大家可以在StackOverflow上的一篇问答中了解更多:
why-numpy-instead-of-python-lists
NumPy 是 Python 在科学计算领域取得成功的关键之一,如果你想通过 Python 学习数据科学(例如scipy)或者机器学习(例如numpy),就必须学习 NumPy。
安装并引入Numpy科学计算包模块¶
使用pip, 我们在终端输入
sudo pip3 install numpy
即可安装完成numpy.
引入numpy模块
import numpy
一般来讲习惯上, 我们引入numpy模块的时候, 会将numpy起一个别名
np, 方便调用(因为比较简短)
import numpy as np
ndarray初始化¶
方法1-基础定义¶
接下来, 我们就写一组简单的代码, 实验一下ndarray的相关属性.
首先我们需要使用np.array 函数初始化几个数组.
import numpy as np # 一维数组 A1 = np.array([1, 2, 3]) # 二维数组 A2 = np.array([[1, 2, 3], [4, 5, 6]])
声明数组的方法就是使用[]嵌套, ,分割同层级的元素.
当然有了二维数组, 后面也会有更高维度的数组(或者说是矩阵).
打印一下这两个数组.
print('A1: \n%s'%A1) print('A2: \n%s'%A2)
[OUT]
A1: [1 2 3] A2: [[1 2 3] [4 5 6]]
方法2-初始化特定区间的整数数组¶
初始化一个数组的方式, 我们还可以使用"批量"的方式
np.arange的使用方法类似Python原生的range
它的函数原型为
arange([start,] stop[, step,], dtype=None)
start : 数值区前开始 默认是0stop : 数值区间结束step : 数值增加间隔, 默认为1dtype : 数据类型
代码演示
print('\n递增') print(np.arange(0, 10, 1))
OUTPUT
递增 [0 1 2 3 4 5 6 7 8 9]
print(np.arange(10))
OUTPUT
[0 1 2 3 4 5 6 7 8 9]
可以看到上面的两个语句是等同的.
我们接下来实验一下递减
print('\n 递减') print(np.arange(10, 0, -1))
OUTPUT
递减
[10 9 8 7 6 5 4 3 2 1]
方法3-初始化特定区间的浮点数组¶
我们还可以使用linspace在一个数值区间内划分若干个段(浮点数).
# 随机间隔 np.linspace(1,10,5)
OUTPUT
array([ 1. , 3.25, 5.5 , 7.75, 10. ])
ndarray的属性¶
这里给大家展示几个常用的属性.
| 属性名称 | 含义 |
|---|---|
| ndarray.ndim | 数组的维度,等于Rank |
| ndarray.shape | (行数, 列数) |
| ndarray.size | 元素总个数 = 列数 * 行数 |
| ndarray.dtype | 数组元素数据类型 |
| ndarray.itemsize | 数组中每个元素,字节大小 |
print('A2.ndim = %d' % A2.ndim) print('A2.shape') print(A2.shape) print('A2.size = %d' % A2.size) print('A2.dtype = %s'%A2.dtype) print('A2.itemsize = %d'%A2.itemsize)
OUTPUT
A2.ndim = 2 A2.shape (2, 3) A2.size = 6 A2.dtype = int64 A2.itemsize = 8
ndarray数据类型¶
NumPy 的核心是数组(arrays)。具体来说是多维数组(ndarrays).
nd: n-dimension n维的意思
ndarray与我们之前介绍的 list之间巨大的差别在于, numpy的ndarray所有的元素数据类型必须相同. 这是为矩阵运算做保障的.
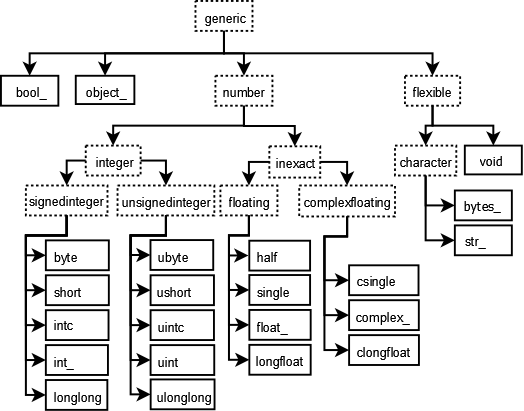
Python支持的数据类型有整型、浮点型以及复数型,但这些类型不足以满足科学计算的需求,因此NumPy中添加了许多其他的数据类型,如bool、inti、int64、float32、complex64等。同时,它也有许多其特有的属性和方法。
在Numpy中定义了24种新的Python基础数据类型, 大多基于C语言的数据类型.
不是所有的ndarray的数据类型, 都可以交给
python-opencv计算的, 所以数据类型, 在使用的时候也要注意.
我们还可以使用astype函数, 将原本为int类型的ndarray转换为浮点型.
# 修改数据格式 A2.astype(float)
OUTPUT
array([[ 1., 2., 3.],
[ 4., 5., 6.]])
slicing切片操作¶
何为切片? 大家应该吃过面包吧

一开始这里是一个大大的面包, 而我们需要这一整个面包其中的一部分, 所以,为了达到这个目的, 我们要进行切片, 可以横着切, 也可以竖着切, 于是我们就获取到了面包片.同样对于多维数组, 我们切片是为了获取数组的其中某一个子区域.
一维数组切片¶
Numpy 中多维数组的切片操作与 Python 中 list 的切片操作一样,同样由 start, stop, step 三个部分组成.
首先我们声明一个长度为10的一维数组.
A = np.arange(10)
OUTPUT 打印一下A
In [7]: A
Out[7]: array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
那么我们需要获取, 前三个元素.
我们输入A[:3], 使用:分隔, 第一个参数是起始值, 默认为0, 这里可以省略.
后面的3是切片的结尾(但是取不到编号为3的元素)
In [8]: A[:3] Out[8]: array([0, 1, 2])
完整版是这种写法:
In [11]: A[0:3] Out[11]: array([0, 1, 2])
:分割的第三个参数是step代表每次走多少步, 即序号增加的数值, 默认为1.
所以更完整的写法是:
In [12]: A[0:3:1] Out[12]: array([0, 1, 2])
我们也可以隔一个数值取一个. 我们设置step=2
In [13]: A[0:10:2] Out[13]: array([0, 2, 4, 6, 8])
step也可以是负值, 例如我们设置为step=-1
In [15]: A[-1:5:-1] Out[15]: array([9, 8, 7, 6])
需要说明的是, 这里start=-1 代表是最末尾的元素.
如果我们只是填写step=-1 结果等于原来数组的倒序
In [14]: A[::-1] Out[14]: array([9, 8, 7, 6, 5, 4, 3, 2, 1, 0])
多维数组切片¶
针对多维数组的切片, 不同之处在于, 需要使用,分隔.
一图胜千言, 相信大家看下面这张图片就会秒懂.

ndarray的内存共享¶
ndarray的之间的直接赋值与索引(切片 slicing)赋值, 那么这两个元素之间的所使用的内存都是同一块.
也就意味着, 如果A = B, 修改B的值, A也会被修改, 因为他们共用了同一片内存空间.
这样比较高效, 但是如果不注意的话, 也会造成很多问题.
我们先来演示一下.
In [1]: import numpy as np In [2]: A = np.array([[1, 2], [3, 4]]) In [3]: A Out[3]: array([[1, 2], [3, 4]]) In [4]: B = A In [5]: B[0] = -1 In [6]: B Out[6]: array([[-1, -1], [ 3, 4]]) In [7]: A Out[7]: array([[-1, -1], [ 3, 4]])
ndarray的深度拷贝¶
那么, 我们如何才可以复制一个ndarray, 修改新的ndarray而不影响之前的值呢?
这里我们需要用到numpy的深度拷贝函数. np.copy
new_img = np.copy(old_img)
In [8]: A = np.array([[1, 2], [3, 4]]) In [9]: B = np.copy(A) In [10]: B[0] = -1 In [11]: B Out[11]: array([[-1, -1], [ 3, 4]]) In [12]: A Out[12]: array([[1, 2], [3, 4]])
当然我们也可以使用另外一种拷贝方式:
B = A.copy()
如果你对python中的浅度拷贝跟深度拷贝不是很清楚的话, 可以看一下博客园的这篇文章.
顺便你再了解一下copy包里面的copy 跟deepcopy 两个函数都有哪些不同.

ndarray的变形¶

在矩阵计算中, 有时候我们需要将矩阵进行变形, 例如原来是4*5的矩阵, 可能会变形为5*4 或者10*2.
也有可能为改变维度, 原来是二维的转变为一维的, 例如1*20.
这里我们就需要两个函数resize 跟reshape
reshape¶
reshape函数的原型:
reshape(a, newshape, order='C')
其中 a 是要被resize的数组
new_shape是新数组的尺寸, 类型为tuple 元组类型
使用样例
In [29]: A = np.arange(10) In [30]: A Out[30]: array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9]) In [31]: np.reshape(A, (2, 5)) Out[31]: array([[0, 1, 2, 3, 4], [5, 6, 7, 8, 9]])
reshape函数变形前与变形后的size必须相同.
否则就会报错.
In [21]: np.reshape(A, (5, 5)) --------------------------------------------------------------------------- ValueError Traceback (most recent call last) <ipython-input-21-a0bcf970fe78> in <module>() ----> 1 np.reshape(A, (5, 5)) /usr/lib/python3.6/site-packages/numpy/core/fromnumeric.py in reshape(a, newshape, order) 230 [5, 6]]) 231 """ --> 232 return _wrapfunc(a, 'reshape', newshape, order=order) 233 234 /usr/lib/python3.6/site-packages/numpy/core/fromnumeric.py in _wrapfunc(obj, method, *args, **kwds) 55 def _wrapfunc(obj, method, *args, **kwds): 56 try: ---> 57 return getattr(obj, method)(*args, **kwds) 58 59 # An AttributeError occurs if the object does not have ValueError: cannot reshape array of size 10 into shape (5,5)
ndarray对象A在调用reshape函数的时候, 返回一个新的ndarray对象, 原来的ndarray并不发生改变.
In [23]: A Out[23]: array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9]) In [24]: A.reshape((2, 5)) Out[24]: array([[0, 1, 2, 3, 4], [5, 6, 7, 8, 9]]) In [25]: A Out[25]: array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
resize¶
resize相当于reshape的一种扩展, 他不要求新的array的size 必须与原来array的size相同, 可以自动填充.
np.resize的函数原型
resize(a, new_shape)
其中 a 是要被resize的数组
new_shape是新数组的尺寸, 类型为tuple 元组类型
我们首先声明一个1*10的一维数组
In [6]: A = np.arange(10) In [7]: A Out[7]: array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
将其转换为2维数组.
In [17]: np.resize(A, (2, 5)) Out[17]: array([[0, 1, 2, 3, 4], [5, 6, 7, 8, 9]])
如果
new_shape 大于a的shape, 则使用a填充.
In [18]: np.resize(A, (4, 5)) Out[18]: array([[0, 1, 2, 3, 4], [5, 6, 7, 8, 9], [0, 1, 2, 3, 4], [5, 6, 7, 8, 9]])
In [19]: np.resize(A, (5, 5)) Out[19]: array([[0, 1, 2, 3, 4], [5, 6, 7, 8, 9], [0, 1, 2, 3, 4], [5, 6, 7, 8, 9], [0, 1, 2, 3, 4]])
ndarray对象A在调用resize函数的时候, 什么也不返回, 原来的ndarray值变更为resize之后的.
In [25]: A Out[25]: array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9]) In [26]: A.resize((2, 5)) In [27]: A Out[27]: array([[0, 1, 2, 3, 4], [5, 6, 7, 8, 9]])
矩阵拼接¶
在opencv中常会用到图像拼接, 这里就需要用到numpy中的矩阵拼接.
矩阵拼接有个前提条件, 就是,拼接的那一面长度必须相同.
-
hstack() 横向拼接
-
vstack() 纵向拼接
我们先声明两个矩阵, A, 跟B
A = np.arange(16).reshape(4,4) B = np.arange(16).reshape(4,4) * -1 print(A) print(B)
OUTPUT
[[ 0 1 2 3]
[ 4 5 6 7]
[ 8 9 10 11]
[12 13 14 15]]
[[ 0 -1 -2 -3]
[ -4 -5 -6 -7]
[ -8 -9 -10 -11]
[-12 -13 -14 -15]]
然后将两个矩阵先进行横向拼接. 注意这里传入的是tuple
# 注意这里传入的是tuple np.hstack((A, B))
OUTPUT
array([[ 0, 1, 2, 3, 0, -1, -2, -3],
[ 4, 5, 6, 7, -4, -5, -6, -7],
[ 8, 9, 10, 11, -8, -9, -10, -11],
[ 12, 13, 14, 15, -12, -13, -14, -15]])
然后再尝试进行纵向拼接.
np.vstack((A, B))
OUTPUT
array([[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11],
[ 12, 13, 14, 15],
[ 0, -1, -2, -3],
[ -4, -5, -6, -7],
[ -8, -9, -10, -11],
[-12, -13, -14, -15]])
ufunc 全局函数¶
作用于数组中每个元素的函数我们称之为ufunc
universal function # 全局函数
在ufunc中,如果是两个ndarray之间的运算,shape必须相等
-
+加法 -
-减法 -
*乘法, 注意这里不是点乘 -
/除法
声明两个尺寸相同的矩阵. A 与B
In [54]: A = np.arange(12).reshape((4, 3)) In [55]: B = np.arange(2, 14).reshape(4, 3) In [56]: A Out[56]: array([[ 0, 1, 2], [ 3, 4, 5], [ 6, 7, 8], [ 9, 10, 11]]) In [57]: B Out[57]: array([[ 2, 3, 4], [ 5, 6, 7], [ 8, 9, 10], [11, 12, 13]])
全局加法¶
In [58]: A + B Out[58]: array([[ 2, 4, 6], [ 8, 10, 12], [14, 16, 18], [20, 22, 24]])
全局减法¶
In [59]: A - B Out[59]: array([[-2, -2, -2], [-2, -2, -2], [-2, -2, -2], [-2, -2, -2]])
全局乘法¶
In [60]: A * B Out[60]: array([[ 0, 3, 8], [ 15, 24, 35], [ 48, 63, 80], [ 99, 120, 143]])
全局除法¶
In [61]: A / B Out[61]: array([[ 0. , 0.33333333, 0.5 ], [ 0.6 , 0.66666667, 0.71428571], [ 0.75 , 0.77777778, 0.8 ], [ 0.81818182, 0.83333333, 0.84615385]])
其他全局函数¶
如果我们的计算对象是单个ndarray中的每个元素, 就需要使用到numpy内置的一些全局函数.
例如np.sin() , 这个函数的作用就是返回一个矩阵, 其中每个元素都是原来矩阵A 进行sin运算的结果
print(np.sin(A))
[[ 0. 0.84147098 0.90929743 0.14112001]
[-0.7568025 -0.95892427 -0.2794155 0.6569866 ]
[ 0.98935825 0.41211849 -0.54402111 -0.99999021]
[-0.53657292 0.42016704 0.99060736 0.65028784]]
自定义全局函数¶
我们也可以自定义自己的ufunc 具体方法见
需要先写用C底层实现方法, 然后再python中调用.
先MARK一下, 也想实现自己的C语言拓展, 嘿嘿, 不过暂时没有想到啥应用场景.
broadcasting 广播¶
那如果两个ndarray的shape 不相同的话, 两者之间可以进行计算么?
答案是可以的, shape不同的两个ndarray的操作都是由broadcasting管理的
![]()
举个最简单的例子.
ndarray与数值的运算¶
声明一个矩阵A
In [62]: A = np.array([1, 2])
In [65]: A + 3 Out[65]: array([4, 5])
很明显, A 与3 两个对象的尺寸 显然不相同, 但是二者之间可以进行运算, A中的每个元素都与3进行了加运算.
同样, 减法-, 乘法* ,除法/ 都是成立的.
In [66]: A - 3 Out[66]: array([-2, -1]) In [67]: A * 3 Out[67]: array([3, 6]) In [68]: A / 3 Out[68]: array([ 0.33333333, 0.66666667])
ndarray与ndarray之间的广播¶
两个ndarray进行广播由个前提条件, 就是其中一个的shape应该是(N, 1) 另外一个是(1, N)
有趣的是一维的ndarray的矩阵转置的尺寸并不是(N, 1)
In [87]: A.shape Out[87]: (2,) In [88]: A.T.shape Out[88]: (2,)
所以, 我们先将矩阵A进行转置, 并且reshape为 (N, 1)
In [78]: C = np.reshape(A.T, (2,1))
OUTPUT
In [90]: C
Out[90]:
array([[1],
[2]])
In [91]: B
Out[91]: array([2, 4, 6])
加法广播¶
然后尝试B与C进行加法运算.
In [92]: C + B Out[92]: array([[3, 5, 7], [4, 6, 8]]) In [93]: B + C Out[93]: array([[3, 5, 7], [4, 6, 8]])
可以看到C + B 与B + C计算的值是相等的.
广播的意思是, C中的元素, 分别与B中的元素进行向加, 最后将这些值存在一起.
加入shape为(N, 1) 的矩阵与(1, M)的矩阵进行广播运算, 那么会后获取的矩阵shape 为(N, M).
减法广播¶
这里可以看到C-B的结果与B-C的不同.
C - B 是C中的元素分别减去B中的元素的广播.
B - C 是B中的元素分别减去C中的元素的广播.
In [94]: C - B Out[94]: array([[-1, -3, -5], [ 0, -2, -4]]) In [95]: B - C Out[95]: array([[1, 3, 5], [0, 2, 4]])
乘法广播¶
In [96]: C * B Out[96]: array([[ 2, 4, 6], [ 4, 8, 12]]) In [97]: B * C Out[97]: array([[ 2, 4, 6], [ 4, 8, 12]])
除法广播¶
In [98]: C / B Out[98]: array([[ 0.5 , 0.25 , 0.16666667], [ 1. , 0.5 , 0.33333333]]) In [99]: B / C Out[99]: array([[ 2., 4., 6.], [ 1., 2., 3.]])
np.linalg 线性代数的基本操作¶

numpy的linalg里包含着线形代数的函数.
引入linalg模块
引入并起名为LA
import numpy.linalg as LA
声明一个矩阵A
In [117]: A = np.random.rand(16).reshape((4, 4)) In [118]: A Out[118]: array([[ 0.70961003, 0.38232282, 0.3333471 , 0.67033575], [ 0.42843928, 0.10718751, 0.60270476, 0.17157395], [ 0.59779218, 0.49990817, 0.38124034, 0.40720553], [ 0.39828826, 0.25732704, 0.21937875, 0.73758145]])
矩阵转置¶
In [120]: A.T Out[120]: array([[ 0.70961003, 0.42843928, 0.59779218, 0.39828826], [ 0.38232282, 0.10718751, 0.49990817, 0.25732704], [ 0.3333471 , 0.60270476, 0.38124034, 0.21937875], [ 0.67033575, 0.17157395, 0.40720553, 0.73758145]])
矩阵求逆¶
In [119]: LA.inv(A) Out[119]: array([[ 5.66701404, -0.28541964, -2.31329719, -3.80682588], [-3.70856223, -1.21853464, 4.49424461, 1.17271036], [-3.13121486, 2.0909343 , 1.02248164, 1.79485974], [-0.83498553, -0.04266018, -0.62290378, 2.46845944]])
矩阵乘法¶
另外声明一个矩阵B
In [121]: B = np.random.rand(12).reshape((4, 3))
In [123]: B Out[123]: array([[ 0.53177202, 0.2393353 , 0.28119078], [ 0.65747444, 0.07336546, 0.05293755], [ 0.61559046, 0.86580537, 0.91073328], [ 0.95129791, 0.14128977, 0.36143378]])
矩阵相乘 dot
In [124]: A.dot(B) Out[124]: array([[ 1.47161254, 0.58120931, 0.76564731], [ 0.8325423 , 0.65647117, 0.73706332], [ 1.26862768, 0.56736268, 0.68894366], [ 1.21769166, 0.40835537, 0.59199963]])
行列式求解¶
determinant
In [126]: LA.det(A) Out[126]: -0.024091509709235282
np.random 随机函数模块¶
生成0-1区间的随机数¶
print('\n生成10个0-1区间内的随机数值\n') print(np.random.rand(10))
OUTPUT
生成10个0-1区间内的随机数值
[ 0.62092807 0.79909637 0.29885985 0.3382252 0.50991553 0.1246462
0.15690747 0.57804792 0.11380593 0.75276443]
生成满足正态分布的数组¶
print('\n生成10个满足正态分布的随机数组\n') print(np.random.randn(10))
OUTPUT
生成10个满足正态分布的随机数组
[-0.77878196 0.08298678 -1.1126773 -0.34096876 -1.39003661 -1.36326881
1.14411379 -0.80727601 -0.94789066 0.01724758]
拓展阅读¶
codingpy - 使用 Python 进行科学计算:NumPy入门
语言比较风趣幽默, 翻译自另外一片英文文章


